黄金図形
2015-06-25 by Horizon Blue Owl
黄金図形
人が自然と安定感や好ましさを覚えるという比率、「黄金比」=1:約1.618。
正確にいうと 1:(1+√5)/2 です。
無理数なので、整数が確定しないのですね。
(1+√5)/2 は φ(ファイ) という記号で表現されることもあります。
2辺の比が黄金比となっている長方形を「黄金長方形」といい、
名刺にはこれに近い形が採用されています。
黄金長方形を作図するには
まず正方形を書き、底辺の中点Aから角Bまでを半径として弧を描きます。
そして正方形の底辺を弧の接点Cまで延長し、長方形の底辺をつくります。
この作図を逆に考えると、黄金長方形から正方形を除いていけば
残った長方形はまた黄金長方形となり、
その黄金長方形からまた正方形を除くと……と永遠に
相似した黄金長方形ができることになります。
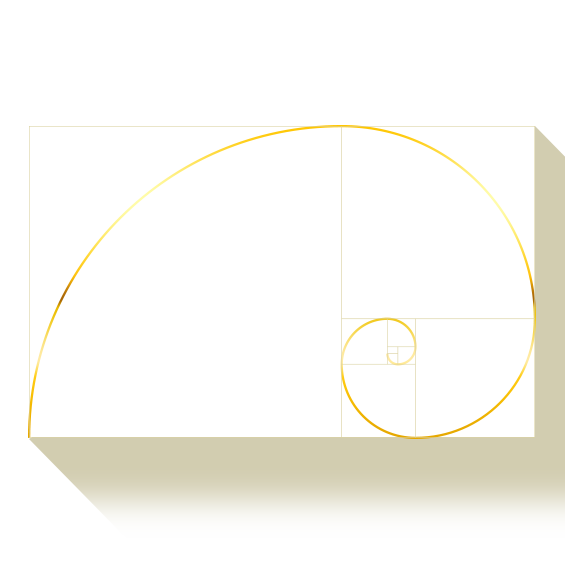
そしてそれぞれの正方形の角をなめらかにつないでいくと、
まるでアンモナイトの殻のような渦巻を描くことができます。
これを「黄金螺旋」といいます。
アンモナイトのような、と例えを出しましたが
実際に巻貝やバラの花びら、ひまわりの中心部分、松ぼっくりなどは
まるで黄金比に則ったかのような成長プロセスを踏みます。
自然界において普遍的な法則だからこそ美しいと感じられるのでしょうか。
古代ギリシャの建築物や美術作品では、多くの部分で
黄金比が見られることは有名ですね。
現在でも、比率を決めるのに黄金比を流用したり
黄金螺旋を参考に構図をとったりと
